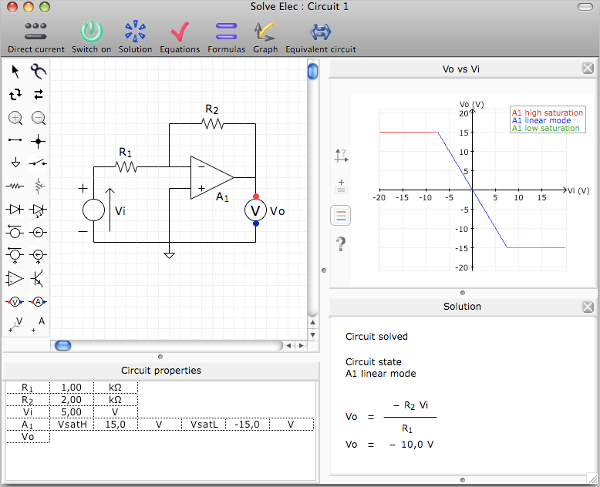
tinysoli.blogg.se - Solve elec oscillateur

#Solve elec oscillateur free#

#Solve elec oscillateur free#

van der Pol: "A theory of the amplitude of free and forced triode vibrations", Radio Review (later Wireless World) 1 701–710 (1920) Journal of the London Mathematical Society.

^ Heitmann, S., Breakspear, M (2017-2022) Brain Dynamics Toolbox.

The relationship between the classical Stuart–Landau model ( μ→0) and more general limit-cycle oscillators (arbitrary μ) has also been demonstrated numerically in the corresponding quantum models. The quantum Stuart–Landau model has played an important role in the study of quantum synchronisation (where it has often been called a van der Pol oscillator although it cannot be uniquely associated with the van der Pol oscillator). The form of the classical Stuart–Landau equation is much simpler, and perhaps not surprisingly, can be quantized by a Lindblad equation which is also simpler than the Lindblad equation for the van der Pol oscillator.

The Stuart–Landau equation in fact describes an entire class of limit-cycle oscillators in the weakly-nonlinear limit. μ→0) the van der Pol oscillator reduces to the Stuart–Landau equation. Note the above Hamiltonian approach with an auxiliary second-order equation produces unbounded phase-space trajectories and hence cannot be used to quantize the van der Pol oscillator. The quantum van der Pol oscillator, which is the quantum mechanics version of the classical van der Pol oscillator, has been proposed using a Lindblad equation to study its quantum dynamics and quantum synchronization. Such a Hamiltonian also connects the geometric phase of the limit cycle system having time dependent parameters with the Hannay angle of the corresponding Hamiltonian system.

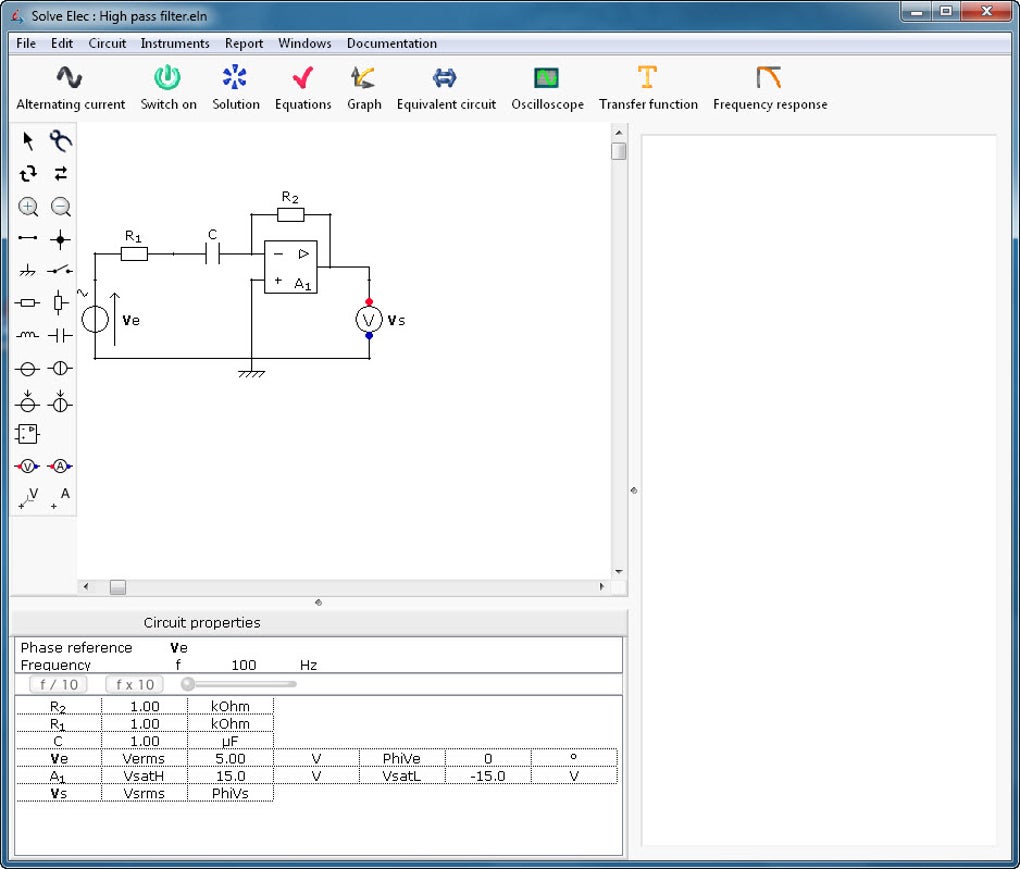
This may, in principle, lead to quantization of the Van der Pol oscillator. Those self-sustained oscillations are of the greatest importance in clock-making, musical instruments, wireless telegraphy, friction dynamics, chemistry, biology and many other fields.Īlmost simultaneously and independently in the beginning of the years 1880, Lord Rayleigh proposed a second order differen¬ tial equation with a suitable nonlinear friction term, to modelize self-sustained oscillations, and Henri Poincaré showed the pres¬ ence, in planar systems of nonlinear differential equations, of periodic solutions to which neighboring solutions are asymptotic for t going to infinity, named limit cycles.D 2 x d t 2 − μ ( 1 − x 2 ) d x d t + x = 0, are the conjugate momenta corresponding to x and y, respectively. able to transform a continuous source of energy into a periodic motion exist since Antiquity, and the most ludic one can be the drinking bird, a scientific toy patented by an American inventor in 1946. Devices producing self-sustained oscillations, i.e. The aim of this work is to sketch and, sometimes, to refine the history of the notion of self-sustained oscillations or auto-oscilla¬ tions in science and technology, and that of the mathematical concept of limit cycle of a system of ordinary differential equa¬ tions. Can the drinking bird explain economic cycles?Ī history of auto-oscillations and limit cyclesĭedicated to the memory of my thesis adviser, Paul Ledoux 1.